Modelado de sistemas de ingeniería en espacio de estados

Introducción

El modelado en espacio de estados es un procedimiento para la construcción de un modelo matemático a partir de un modelo físico que se rige por las leyes naturales conocidas, por ejemplo, las leyes de Newton. Este tipo de modelado permite reconocer la presencia de los componentes y la interconexión adecuada entre ellos a partir del desarrollo del modelo físico que lo rige, asumiendo sus propias relaciones constitutivas.

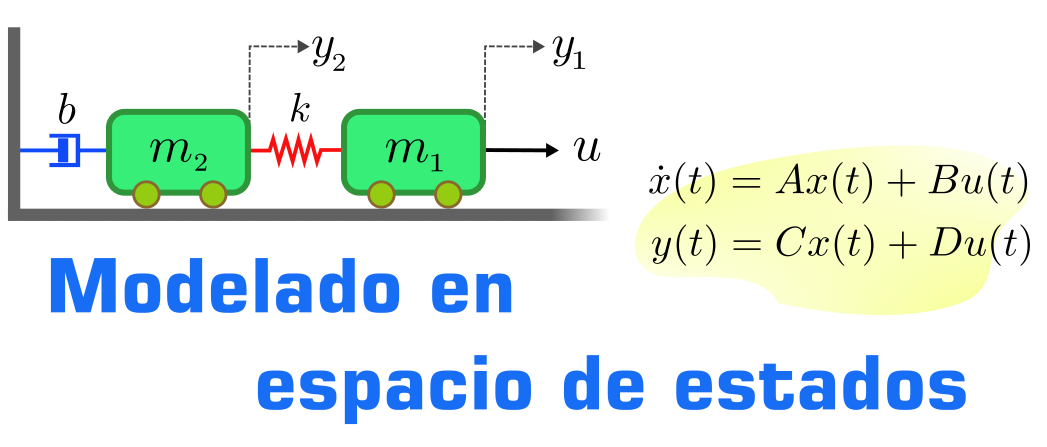
**Figura 1.** *Modelado en espacio de estados*

El enfoque del modelado en espacio de estados considera de manera especial a los modelos de parámetros concentrados de sistemas de ingeniería, en especial sistemas mecánicos y eléctricos, así mismo pertenece al grupo de métodos basados en consideraciones formales de causas y efectos físicos en los componentes de los sistemas. El método resulta atractivo en comparación a los modelos basados en leyes de conservación de la energía, porque proporciona al usuario la oportunidad de desarrollar y aplicar su intuición física.

En el presente tema se abordan los conceptos, procedimientos y ejemplos del modelado de sistemas en ingeniería, en especial, los de tipo mecánico y eléctrico; dichos conocimientos serán de gran utilidad al momento de generar modelos matemáticos para la resolución de problemas concretos en el enfoque en espacio de estados.

Cabe recalcar que el modelado en espacio de estados es el primer paso para la realización de un análisis y diseño de sistemas de control propios del método, con un alcance de aplicación para los sistemas no lineales o variantes en el tiempo; en otras palabras, este tipo de representación permite entender en cierta medida la dinámica interna de un sistema y a su vez otorga la capacidad de controlar su respuesta.

Esta metodología está considerada dentro de la Teoría moderna de control de sistemas dinámicos por utilizar el concepto de estado, a diferencia de la Teoría clásica de control que utiliza solamente el concepto de función de transferencia, que es la razón matemática de la entrada y la salida de un sistema lineal invariante en el tiempo.

Sin más preámbulo, ¡Comenzamos y bienvenidos!

Objetivo: Reconocer los conceptos y metodología del modelado en espacio de estados para deducir y explicar modelos de sistemas de ingeniería propuestos a partir de la teoría y ejercicios prácticos.

Temas que se abordan

1. Conceptos.
1.1 Ecuación de estado y ecuación de salida.
2. Método de obtención del modelo de estado.
2.1 Modelado en espacio de estados con la elección de variables de estado como magnitudes físicas del sistema.
a) Ejemplo 1. Sistema mecánico compuesto por masa, resorte y amortiguador.
b) Ejemplo 2. Sistema mecánico compuesto por masa, resorte y fricción.
c) Ejemplo 3. Sistema eléctrico compuesto por inductor, resistencia y capacitor.
d) Ejemplo 4. Sistema eléctrico compuesto por inductor, capacitor y resistencia en paralelo.

1. Conceptos

Actualmente, las diferentes ramas de control automático, dentro de las que se encuentran el control no lineal, el control adaptativo, el control óptimo, entre otros, convergen en la necesidad de utilizar un modelo matemático que describa el comportamiento del sistema dinámico referente a la evolución de sus variables internas, para su aplicación a sistemas multivariables, no lineales y/o variables en el tiempo. Este tipo de modelado se denomina: Modelado en espacio de estados.

La representación de la dinámica interna se fundamenta en tres conceptos:

Domínguez (2006) las define como:

El concepto de estado de un sistema es la cantidad mínima de información necesaria en un instante de tiempo que, junto con la entrada en ese mismo instante, permite determinar el comportamiento de cualquier variable del sistema en cualquier instante de tiempo posterior (Domínguez, 2006).

Las variables de estado del sistema se definen como la representación de la cantidad mínima de información que define el estado. Este conjunto de variables se define por x_i (t), con i variables necesarias al orden del sistema y cuyos valores dependen del instante del tiempo considerado. Se llama orden del sistema al número de variables de estado con el que se construye.

El conjunto de variables de estado recibe el nombre de vector de estado y se denota por el vector x(t). En muchos de los sistemas físicos reales se puede obtener un modelo aproximado donde el vector de estados es de dimensión finita de orden n (Domínguez, 2006). Este enfoque se verá más adelante.

El espacio de estados se define como el espacio vectorial n-dimensional cuyos ejes de coordenadas corresponden a la n dimensión del vector de estados y en el cual éste último toma valores (Domínguez, 2006).

1.1 Ecuación de estado y ecuación de salida

Una vez que hayas asimilado los tres conceptos fundamentales para la representación de la dinámica interna, el siguiente paso es realizar el modelo matemático de un sistema dinámico utilizando dos ecuaciones: la ecuación de estado y la ecuación de salida. Antes de plantear el procedimiento para la obtención de estas dos ecuaciones vamos a definirlas.

De acuerdo con Domínguez (2006), al trabajar con sistemas físicos reales debemos recordar que el modelado matemático que modela de forma aproximada algunos de los fenómenos físicos con gran precisión es la representación por ecuaciones diferenciales. Por lo tanto, partiendo de esta premisa, un sistema dinámico diferencial puede así ser representado por una ecuación que incluya información del estado, entonces podemos escribir el modelado en espacio de estados mediante las ecuaciones siguientes:

La ecuación de estado es la que representará la evolución del estado del sistema, en función del valor actual del estado y la aportación de la entrada. Las ecuaciones (1) y (2) son la realización del modelado en espacio de estados. En estas ecuaciones f y η son funciones vectoriales. Si el sistema dinámico es lineal las ecuaciones del modelo en espacio de estados se puede expresar en forma matricial como se muestra a continuación:

Las ecuaciones (3) y (4) representan el modelo en espacio de estados de un sistema dinámico lineal donde:

Vamos a iniciar con una serie de ejemplos para mostrar cómo se puede obtener el modelado matemático de diversos sistemas físicos como sistemas modelados en espacio de estados.

2. Método de obtención del modelo de estado

Continuando con el tema y siguiendo la propuesta de Domínguez (2006), se dan a conocer las pautas de un método para el modelado de sistemas físicos con el enfoque del modelado en espacio de estados. Si bien es cierto que la representación del estado no es única, pudiendo encontrar infinitas representaciones, todas ellas son equivalentes e igualmente válidas entre sí para la descripción del sistema.

Considerando las ecuaciones (3) y (4) del sistema que acabamos de ver, de acuerdo con Domínguez (2006), las condiciones que se habrán de tomar en cuenta para elegir un modelo de estado son cuatro:

Algunos métodos descritos en Domínguez (2006) para la elección de variables de estado de un sistema en el modelado en espacio de estados son:

a) Variables de estado como magnitudes físicas del sistema.
b) Variables de estado como salida de los integradores del sistema.
c) Variables de estado de fase.
d) Variables de estado de Jordan.

El método para la asignación de variables de estado que se utilizará en esta UAPA será el del inciso a), pues es considerado el más intuitivo y el que mejor representa la estructura física del sistema a modelar. A continuación, se describen algunos ejemplos de modelado de sistemas mecánicos y eléctricos en el modelado de espacio de estados.

2.1 Modelado de espacio de estados con la elección de variables de estado como magnitudes físicas del sistema

En la elección de variables de estado como magnitudes físicas del sistema, se tienen que identificar los elementos asociados a estas magnitudes.

A este tipo de elementos se les denomina elementos pasivos, y cumplen con la característica de que la energía introducida al sistema no puede exceder la cantidad que el elemento ha almacenado. En otras palabras, son elementos que no son capaces de producir energía.

En general, algunos elementos pasivos tienen la capacidad de almacenar energía de dos tipos: energía potencial y energía cinética. Enseguida veremos unos ejemplos:

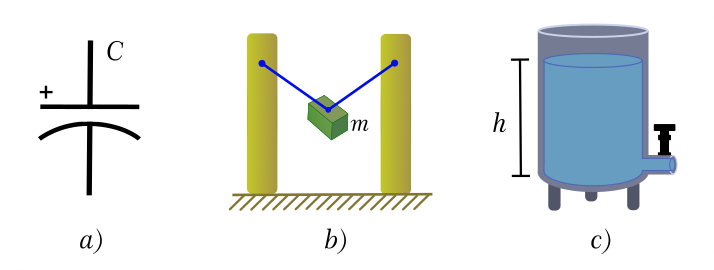
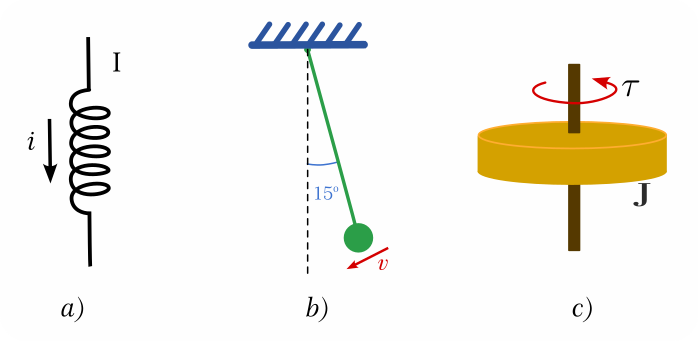
Figura 2. *Ejemplo de elementos que acumulan energía potencial. a) Capacitor, b) masa suspendida a una altura determinada y c) depósito de líquidos*

Nota. De acuerdo con Serway (2008) los conceptos de energía cinética y energía potencial tienen las siguientes características:

Energía cinética

Es un tipo de almacenamiento de energía en el sistema, definida como una cantidad escalar, y está definida en las mismas unidades que el trabajo, esto es, el Julio (J). La energía cinética representa la energía asociada con el movimiento de la masa. La ecuación en el teorema de trabajo-energía cinética para la energía cinética traslacional es

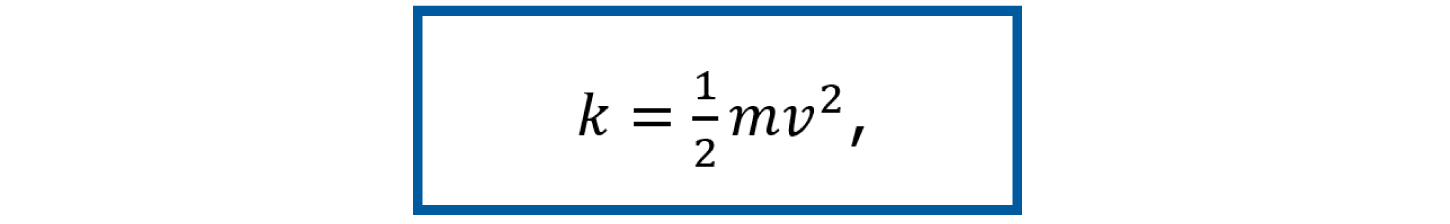
donde m es la masa y v es la velocidad.

Energía potencial

La energía potencial puede ser de tipo gravitacional, donde solamente depende de la altura vertical del objeto sobre la superficie de la tierra. La energía potencial gravitacional para una masa está descrita por

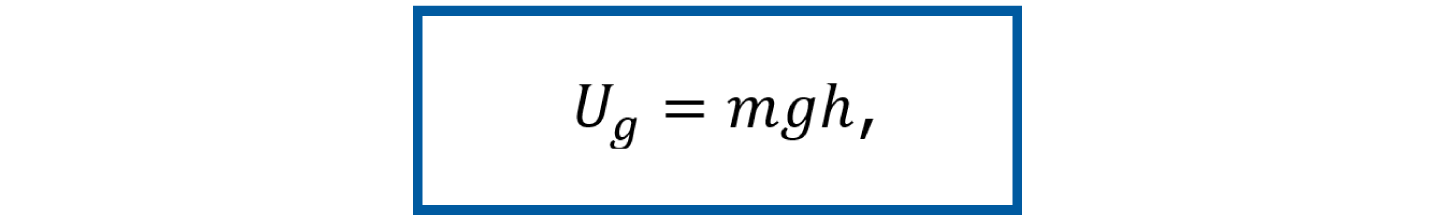
donde m es la masa, g el valor de la gravedad

y h es la altura.

También se tiene la energía potencial elástica, que es la energía almacenada en un resorte cuando el resorte está estirado o comprimido. La energía potencial elástica es proporcional a su desplazamiento al cuadrado, descrita por la ecuación

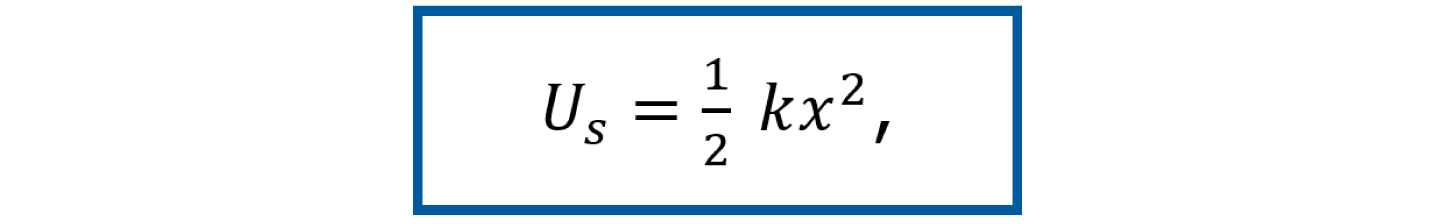
donde k es la constante de elasticidad del resorte y x la distancia del resorte al ser estirado o comprimido.

A continuación se presentan los elementos pasivos agrupados, de acuerdo al tipo de energía almacenada dentro de un sistema mecánico y eléctrico.

Elementos pasivos en sistemas mecánicos

En sistemas mecánicos únicamente los elementos de masa y resorte pueden almacenar energía potencial. Son los elementos de inercia aquellos que permiten almacenar energía cinética. Ogata (1988) nos menciona ejemplos de estos elementos: una masa m en traslación pura a velocidad v, o un momento de inercia J en rotación pura a velocidad angular θ ̇.

Cabe mencionar que los elementos disipadores de energía en sistemas mecánicos son los amortiguadores.

Elementos pasivos en sistemas eléctricos

En los sistemas eléctricos el capacitor puede almacenar energía cuando se le aplica un voltaje entre sus placas, en este caso, esta energía almacenada es en forma de campo eléctrico. El inductor es el elemento capaz de almacenar energía eléctrica como resultado del campo magnético que se genera cuando cierta corriente fluye en él.

Aquí, uno de los elementos disipadores de energía es la resistencia, misma que hace que la energía disipada sea transformada en calor.

Para una identificación rápida y sencilla de los elementos pasivos involucrados en el modelo en espacio de estados, puedes ver en la figura 4 el Esquema de los diferentes elementos pasivos en sistemas mecánicos y eléctricos, que presenta un esquema por tipo de energía almacenada en un sistema mecánico o eléctrico.

Figura 4.Esquema de los diferentes elementos pasivos en sistemas mecánicos y eléctricos

Por otro lado, existen elementos físicos que son denominados activos, pues son capaces de entregar energía externa al sistema. En sistemas mecánicos se encuentran, por ejemplo, las fuerzas y pares externos. En sistemas eléctricos son las fuentes de voltaje y de corriente.

Ahora que ya conoces los elementos que interactúan en un sistema mecánico y en un sistema eléctrico, de acuerdo con su tipo de energía, vamos a introducirnos de lleno en ejemplos de modelado en espacio de estados.

Ejemplo 1. Sistema mecánico compuesto por masa, resorte y amortiguador.

A continuación se muestra paso a paso la manera de obtener una representación del modelado en espacio de estados de un sistema mecánico. El sistema está compuesto por una masa m, un resorte con constante k y un amortiguador con constante b, como el que se muestra en la figura 5, Sistema mecánico masa-resorte-amortiguador.

Figura 5.Sistema mecánico masa-resorte-amortiguador

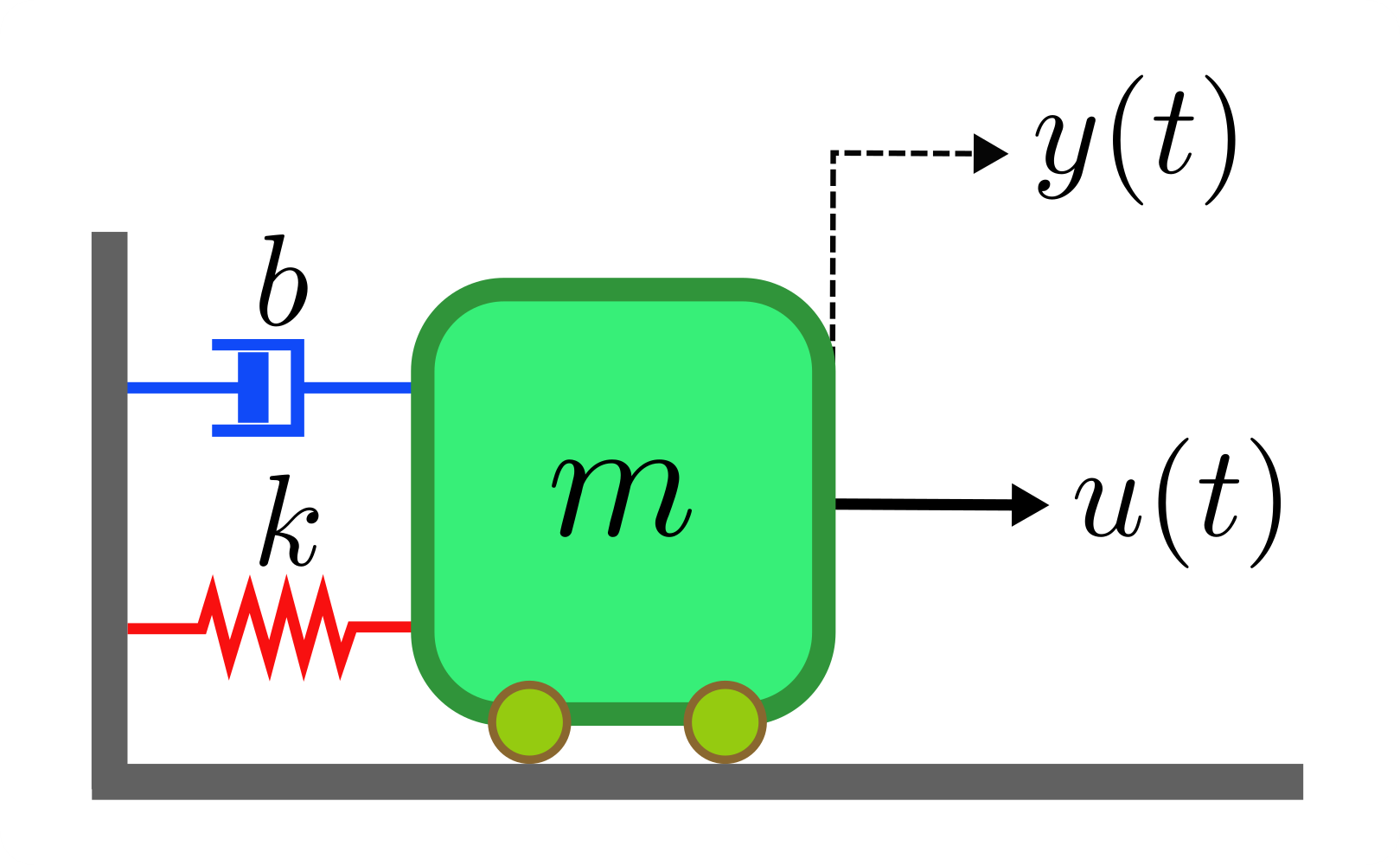
De acuerdo con lo estudiado hasta este momento, se enuncian una serie de pasos para la obtención del modelo en espacio de estados del sistema.

Como primer paso se deben elegir las variables de estado, seleccionando las variables naturales asociadas a cada uno de los elementos acumuladores de energía. Para este sistema mecánico traslacional se seleccionan las variables de estado como la posición y (t ) y la velocidad

de la masa m.

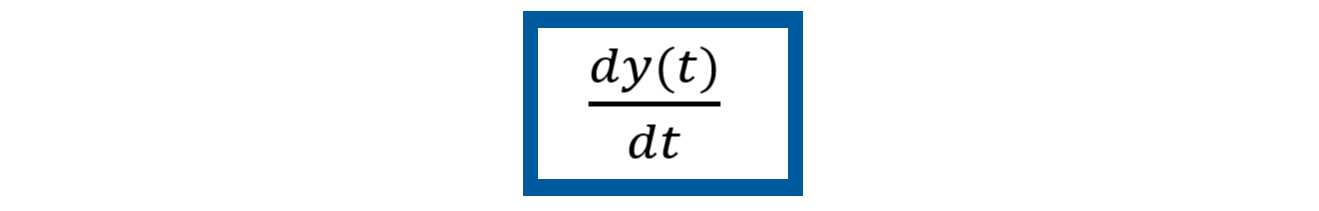
Identificar la variable de salida de interés, respecto el sistema mecánico mostrado en la figura 5, Sistema mecánico masa-resorte-amortiguador. La variable de salida se propone como el desplazamiento y (t ) de la masa m, mismo desplazamiento que estará en función de la entrada u (t ) que se aplica al sistema.

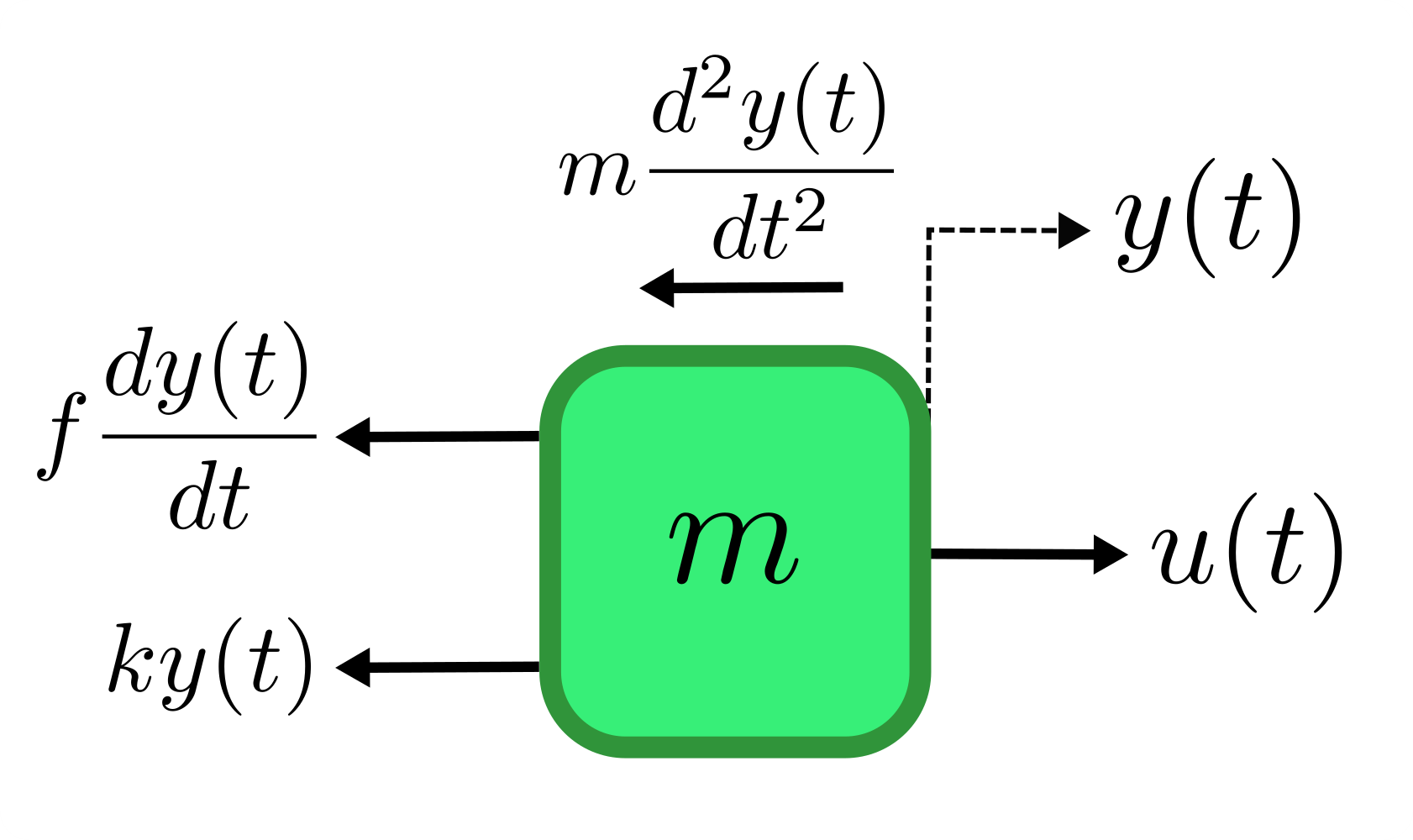
En esta etapa se debe obtener la ecuación dinámica del sistema. En términos de mecánica la base de nuestro análisis son las ecuaciones del movimiento mecánico de las leyes de Newton. En este paso el sistema de la figura 5, Sistema mecánico masa-resorte-amortiguador, se muestra en su diagrama de cuerpo libre, de acuerdo con el método utilizado en Kuo (1996, p. 152) que podrás consultar en el siguiente enlace: https://dademuchconnection.files.wordpress.com/2017/07/sistemas-de-control-automatico-benjamin-c-kuo.pdf, con lo cual se obtiene la figura 6, Diagrama de cuerpo libre del sistema mecánico, del ejemplo 1.

Figura 6. *Diagrama de cuerpo libre del sistema mecánico del ejemplo 1*

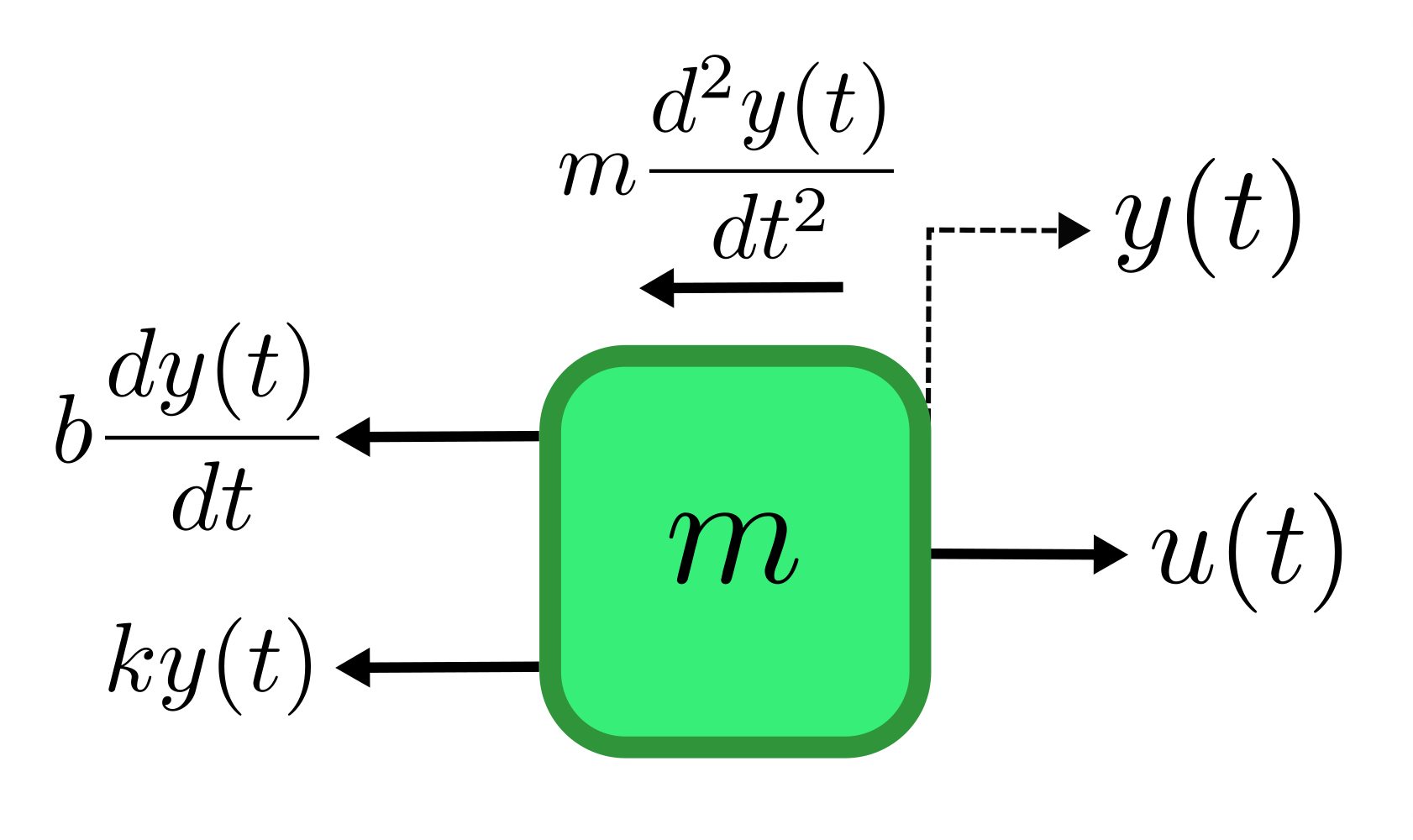
Como se puede observar, la fuerza del amortiguador está en función de la velocidad

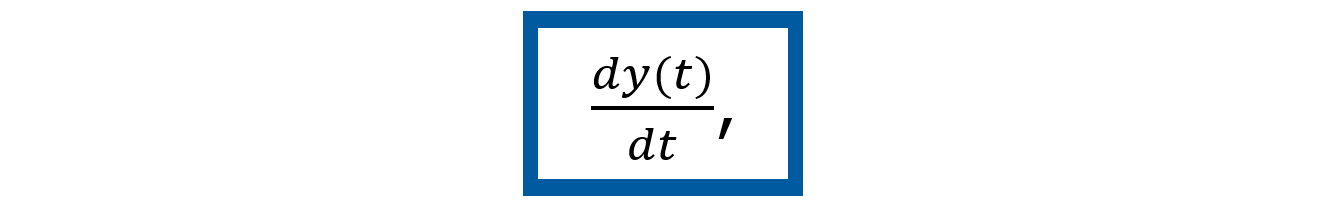
la fuerza del resorte en función de la posición y (t ) y la fuerza de inercia de la masa en función de la aceleración

todas estas fuerzas tienen sentido contrario a la fuerza de excitación, que en este caso, es la entrada u (t ).

Así, utilizando el diagrama de cuerpo libre se obtiene la ecuación dinámica respecto a la sumatoria de las fuerzas del sistema

Sustituyendo las fuerzas de cada elemento con su correspondiente, se llega a la ecuación (5).

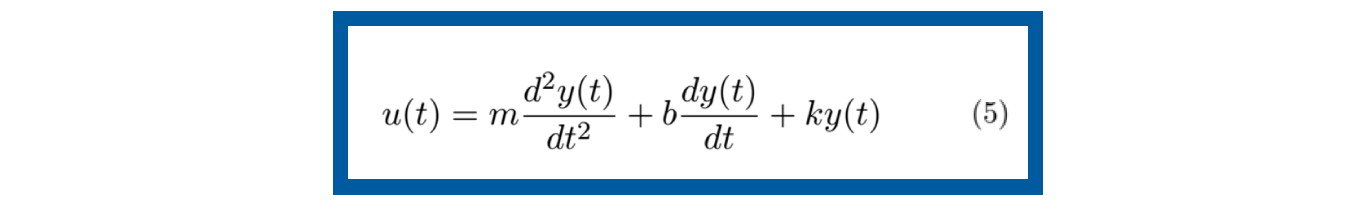
Como se puede ver, la ecuación del sistema es de segundo orden, por tanto, el modelado en espacio de estados indica que se deben de tener dos variables de estado. Como se mencionó en el Paso 1, estas variables de estado son la posición y (t ) y la velocidad de la masa

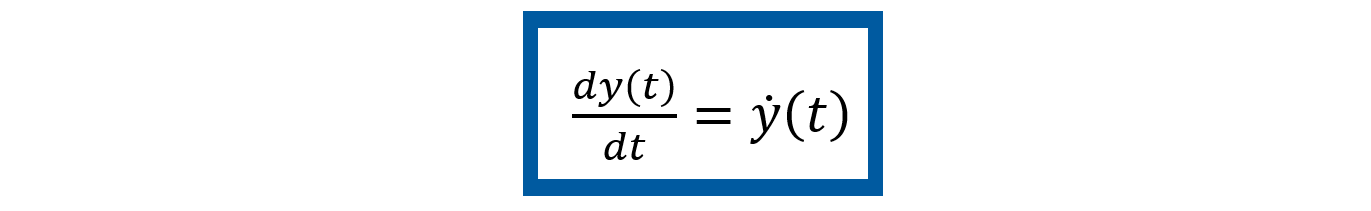
descritas de la siguiente forma por el vector de estado x (t )

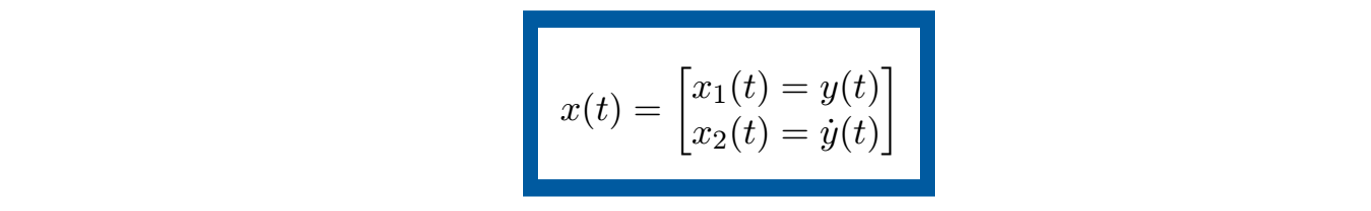
En este paso se toma a la ecuación dinámica del sistema y se procede a describirla en términos del modelo en espacio de estados. Considerando que el sistema es lineal, el modelo en espacio de estados se puede expresar en forma matricial como en las ecuaciones (3) y (4). Simplificando la ecuación dinámica (5) al denotar cada derivada de la variable por un punto como superíndice, esto es: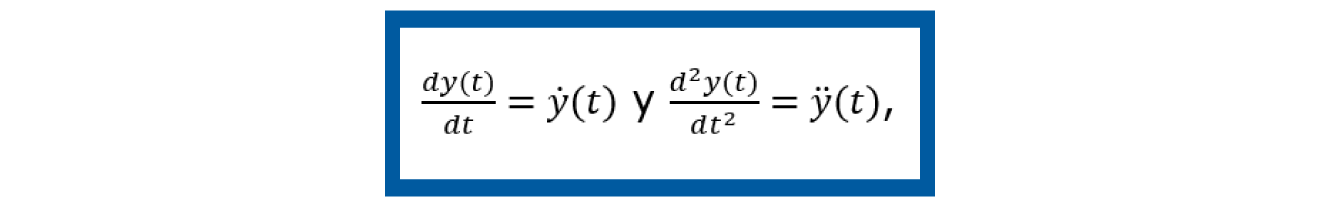

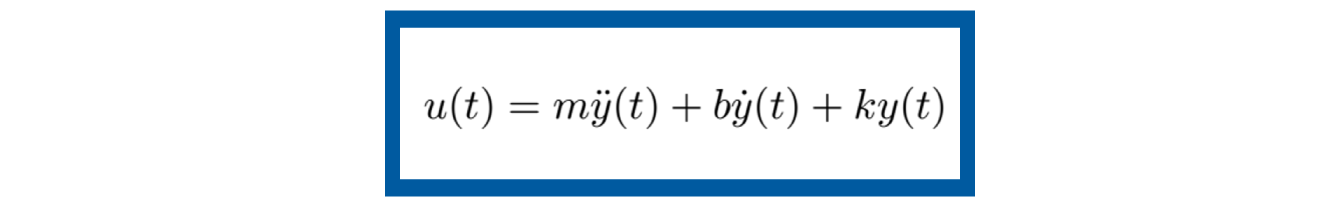
la ecuación se puede reescribir como

Si se despeja la variable de aceleración ÿ (t ) la ecuación dinámica pasa a verse de la siguiente forma

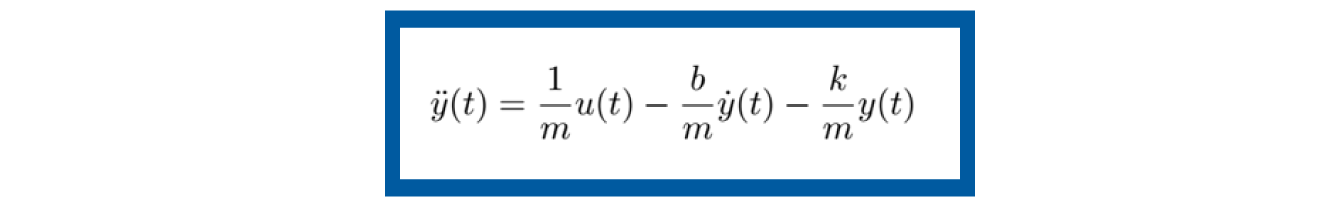
Así entonces, podemos escribir la ecuación de estado ẋ (t ) de la siguiente manera

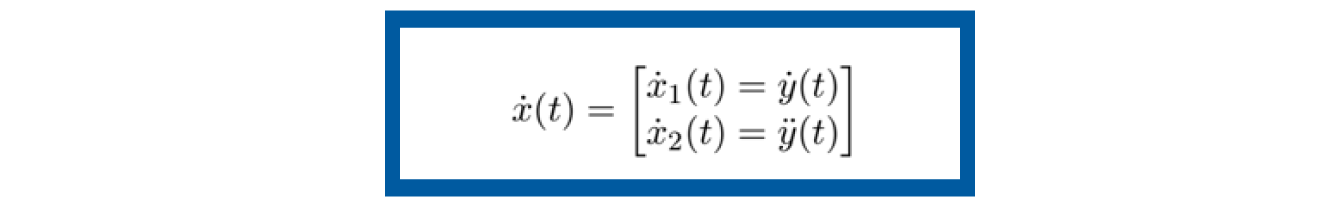
Si acomodamos la ecuación en forma matricial, de acuerdo con el vector de estado y el vector de salida, el resultado es el siguiente

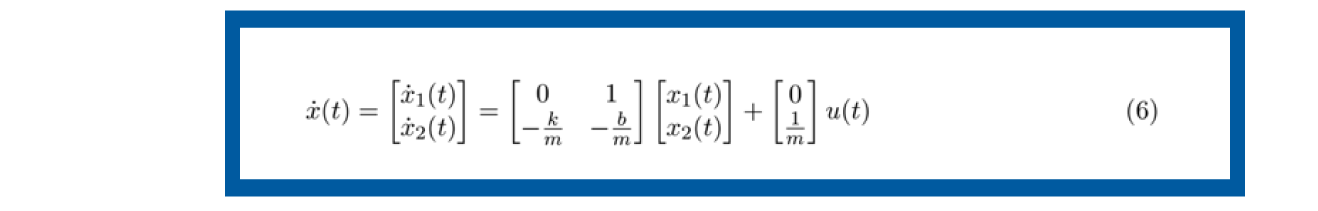
La ecuación de salida y (t ) en forma matricial resulta ser

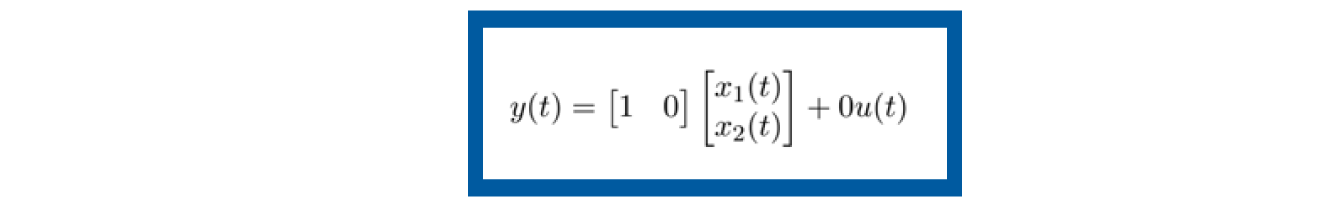
Es importante no confundir la ecuación de salida y (t ) del modelo en espacio de estados, con la variable de salida del sistema que se propuso como el desplazamiento y (t )=x ₁ (t ).

Como se mencionó en los conceptos, la mayoría de los sistemas tiene el segundo término nulo en su ecuación de salida, por lo que podemos escribir simplemente

Así, la ecuación de estado (6) y la ecuación de salida (7) describen de forma matricial el modelado en espacio de estados del sistema mecánico mostrado en la figura 5, Sistema mecánico masa-resorte-amortiguador. Con estas dos ecuaciones damos por finalizado el ejemplo.

NOTA: Recuerda que el número de variables de estado determina el orden del sistema, pero ten en cuenta que, la elección de variables de estado no es única, permitiendo encontrar infinitas representaciones. En este contexto, el modelo de un sistema mecánico donde la posición y la velocidad son seleccionadas como variables de estado, pueden ser cambiadas por la posición y el momento de las masas inerciales.

Ejemplo 2. Sistema mecánico compuesto por masa, resorte y fricción.

En este segundo ejemplo, reafirmaremos tu aprendizaje en el modelado en espacio de estados de sistemas mecánicos mediante una variación en el sistema, con relación al que presentamos en el Ejemplo 1.

Ahora te presentamos el sistema a modelar en espacio de estados, que es un sistema mecánico como se muestra en la figura 7, Sistema mecánico con fricción f. Este sistema tiene un elemento de masa m, un resorte con constante k y la consideración que se encuentra sobre una superficie que provoca fricción. La fricción es considerada en este ejemplo con características similares a un amortiguamiento viscoso de constante f. El desplazamiento a dicho sistema está en función de la entrada u(t ).

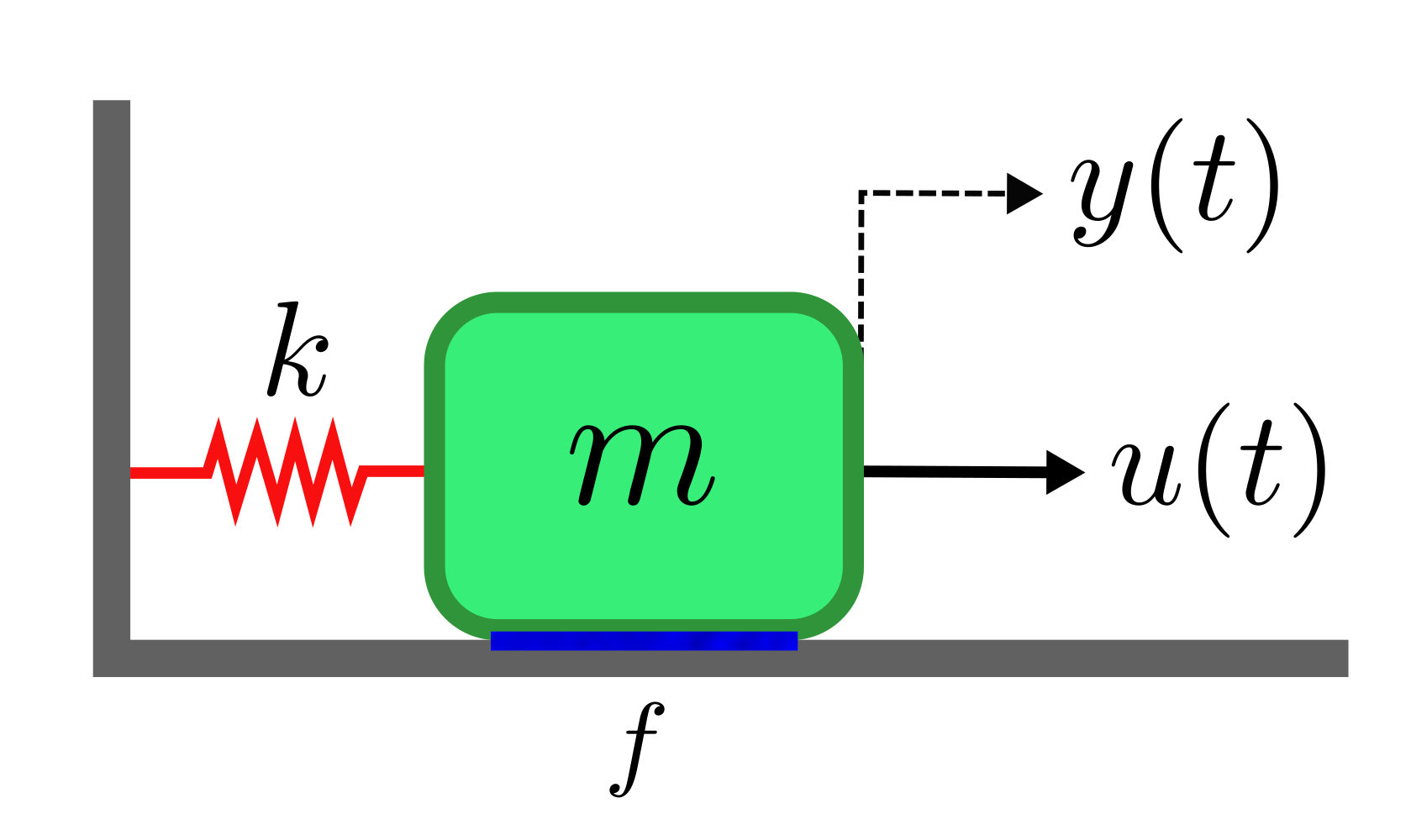
Figura 7.Sistema mecánico con fricción f

Siguiendo la metodología estudiada en este tema, repetiremos la serie de pasos enunciados con anterioridad para la obtención del modelo en espacio de estados de un sistema mecánico, con el fin de consolidar tu aprendizaje en la metodología planteada.

Paso 1

En este primer paso al elegir las variables de estado, notamos que el sistema también presenta las dos variables de estado que en el Ejemplo 1, estas son la posición y (t) y la velocidad

de la masa m. Así, en términos del modelado en espacio de estados se definen estas variables de la siguiente manera

Paso 2

En este paso tenemos que elegir a la variable de salida del sistema. Como se hizo notar anteriormente, la posición y (t ) de la masa m, es la variable de salida de interés.

Paso 3

Con las variables de entrada y salida bien determinadas, es momento de obtener la ecuación dinámica del sistema. Como buena práctica seguiremos desarrollando un diagrama de cuerpo libre para la visualización de los vectores de fuerza que interactúan en el sistema, para la obtención de la ecuación dinámica. Por lo tanto, como se ve en la figura 8, Diagrama de cuerpo libre del sistema mecánico con fricción, se dibujan los vectores de fuerza de cada uno de los elementos que conforman el sistema, en este caso, vemos que el diagrama es bastante parecido al de la figura 7, Sistema mecánico con fricción f.

Figura 8. *Diagrama de cuerpo libre del sistema mecánico con fricción.*

Podemos ver que la fuerza de la inercia de la masa está en función de la aceleración

la fuerza del resorte en función de la posición y (t ), y la fuerza de fricción viscosa está en función de la velocidad

siendo que las tres fuerzas tienen el sentido opuesto a la fuerza de excitación de la entrada u (t ).

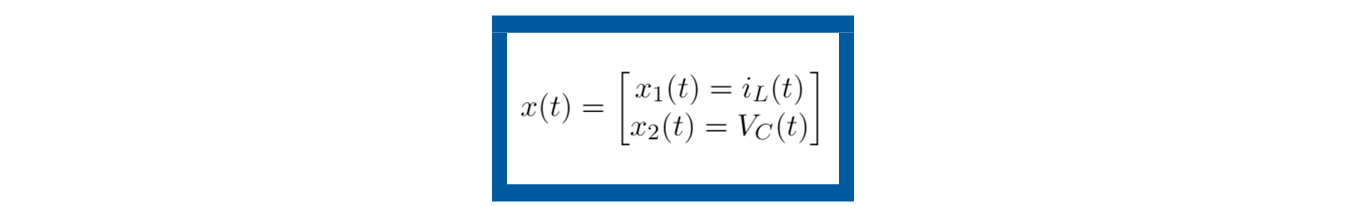
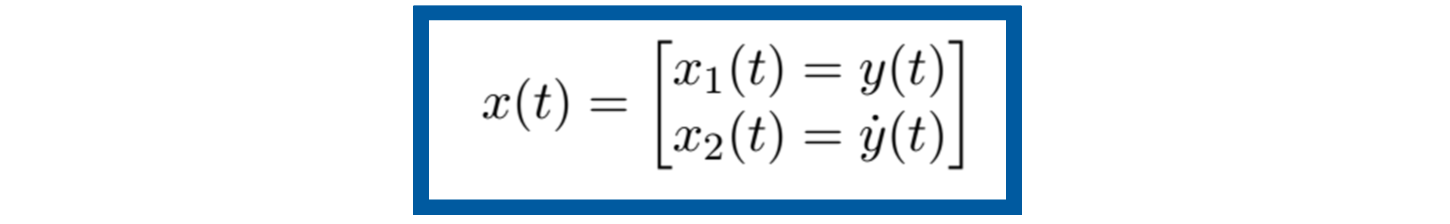
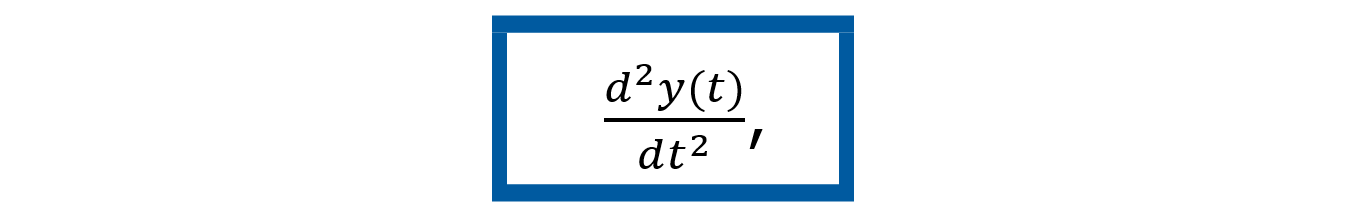
Según el diagrama de cuerpo libre, la ecuación dinámica que describe al sistema mecánico con fricción respecto de la sumatoria de fuerzas del sistema es

Sustituyendo las fuerzas de cada elemento con su correspondiente, se llega a la ecuación (8).

Como se puede ver, la ecuación (8) es la ecuación dinámica del sistema presentado, misma que es de segundo orden, por lo tanto, el modelado en espacio de estados indica que el sistema debe tener dos variables de estado. Recordando el paso uno, se llegó a la determinación de que las dos variables de estado son la posición y (t) y la velocidad de la masa

Paso 4

Es momento de trabajar con la ecuación dinámica y proceder a describirla en términos del modelo en espacio de estados. Para este ejemplo, la ecuación dinámica también puede ser expresada en forma matricial como en las ecuaciones (3) y (4). Trabajando con la ecuación dinámica, ésta puede ser escrita en términos de

de la forma

De igual manera se toma el segundo término de la ecuación de salida con valor nulo. Así, llegamos al resultado de obtener la ecuación de estado (9) y la ecuación de salida (10), que describen de forma matricial el modelado en espacio de estados del sistema mecánico con fricción.

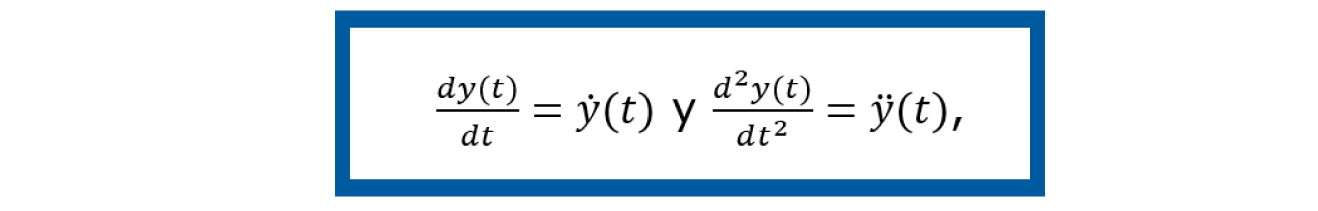
Ejemplo 3. Sistema eléctrico compuesto por inductor, resistencia y capacitor.

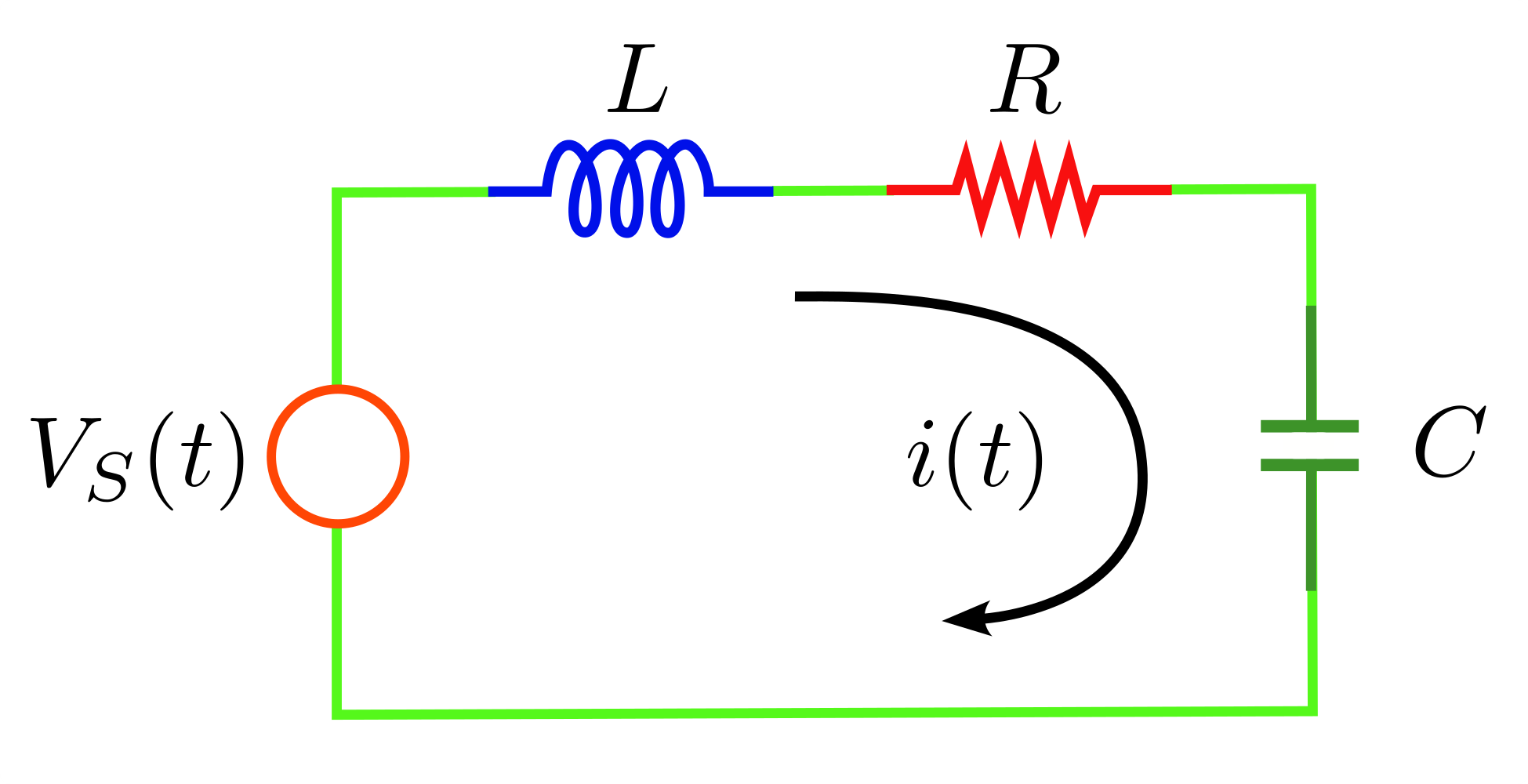
Continuando con sistemas eléctricos, en este ejemplo vamos a obtener paso a paso la representación del modelado en espacio de estados de un sistema eléctrico. El sistema está compuesto por una inductancia L, una resistencia R y un capacitor C, mismos que se encuentran conectados en serie a una fuente de voltaje V_s (t) como se muestra en la figura 9, Sistema eléctrico RLC.

Siguiendo la metodología ya explicada, se presenta la serie de pasos para la obtención del modelo en espacio de estados del sistema.

Como primer paso del modelado elegiremos las variables de estado asociadas al sistema. En sistemas eléctricos, las variables de estado son los voltajes en los capacitores y las corrientes en los inductores. Por lo tanto, la elección de las variables de estado ligadas al sistema de la figura 9, Sistema eléctrico RLC es: el voltaje del capacitor V_c ( t ) y la corriente del inductor i ( t ).

Siguiendo nuestra metodología, como segundo paso se propone la variable de salida. En la figura 9, Sistema eléctrico RLC se tiene que el elemento de lado derecho es el capacitor C, mismo que se ha colocado en esta posición ya que en este tipo de circuitos la variable de interés es su voltaje V_c (t), por lo tanto, será nuestra variable de salida.

En esta etapa se obtienen las ecuaciones dinámicas del sistema. Para esto, es necesario recurrir a las Leyes de voltaje de Kircchoff en la malla del circuito de la figura 9, Sistema eléctrico RLC. Esta ley establece que la suma de todas las diferencias de potencial eléctrico alrededor de una malla es cero, por tanto, en términos matemáticos podemos escribir que

Así, las ecuaciones dinámicas del sistema en la malla, se pueden representar como

Aquí

es el voltaje en la inductancia, V _C ( t ) es el voltaje en el capacitor y Ri(t) es el voltaje en la resistencia. Como se puede observar, la ecuación (12) define la variable de la corriente utilizada en la ecuación (11), aquí la corriente está definida en términos del cambio de voltaje en el capacitor

y el voltaje en el inductor, en términos del cambio de la corriente respecto del tiempo, por tanto, el sistema es de segundo orden; así el modelado en espacio de estados solicita tener dos variables de estado. Como se mencionó antes, estas variables de estado son el voltaje del capacitor V _c ( t ) y la corriente del inductor i ( t ) descritas de la siguiente forma por el vector de estado x ( t )

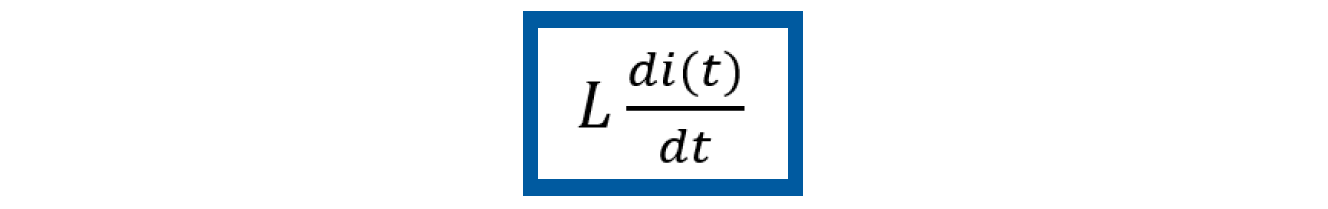
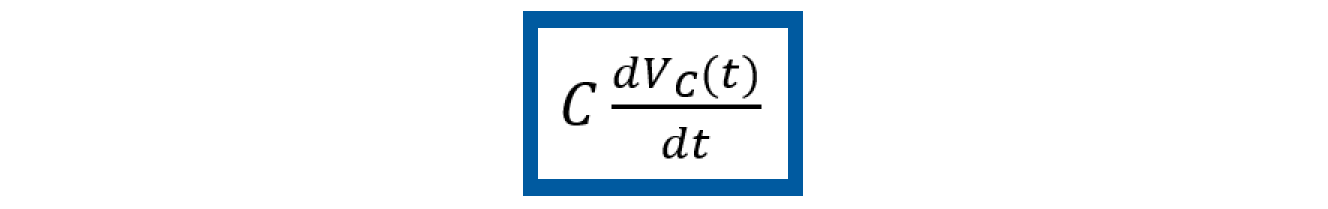
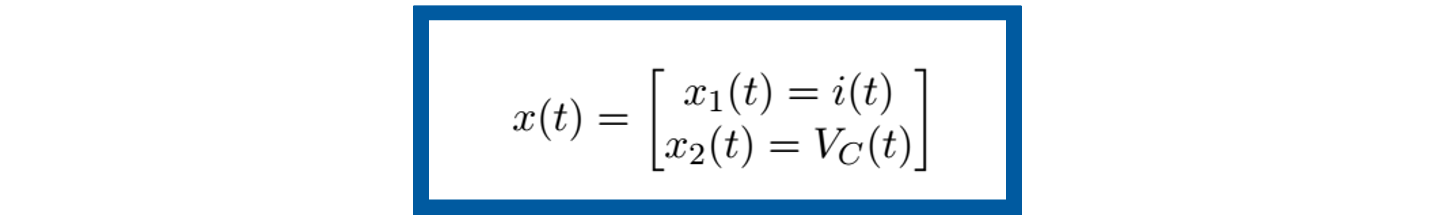
En este paso las ecuaciones dinámicas se describen en términos del modelo en espacio de estados. Considerando que el sistema es lineal, el modelo en espacio de estados se puede expresar en forma matricial, como en las ecuaciones (3) y (4). Por lo tanto, trabajando con las ecuaciones dinámicas (11) y (12) podemos escribir estas ecuaciones despejando los términos diferenciales, con lo cual se obtiene

De esta forma matricial en su forma expandida, de acuerdo con las igualdades de

en términos de las variables de estado, se obtiene la siguiente representación

La ecuación de salida y ( t ) en forma matricial es

Por lo tanto, la ecuación de estado (13) y la ecuación de salida (14) obtenidas, describen de forma matricial el modelado en espacio de estados del sistema mostrado en la figura 9, Sistema eléctrico RLC. Se hacer notar que el uso del modelado en espacio de estados de un sistema eléctrico es muy similar en cuanto a la estructura de sus ecuaciones respecto al modelado de un sistema mecánico, por el hecho de que en ambos sistemas se utilizan variables de estado que representan el estado de los elementos que almacenan energía en su sistema.

Ejemplo 4. Sistema eléctrico compuesto por inductor, capacitor y resistencia en paralelo.

En este último ejemplo, tomado de Chen (1995), se analiza el sistema eléctrico mostrado en la figura 10, Sistema eléctrico, para consolidar tu aprendizaje en el modelado en espacio de estados de sistemas eléctricos y con el doble propósito de retomarlo más adelante en tu actividad de aprendizaje.

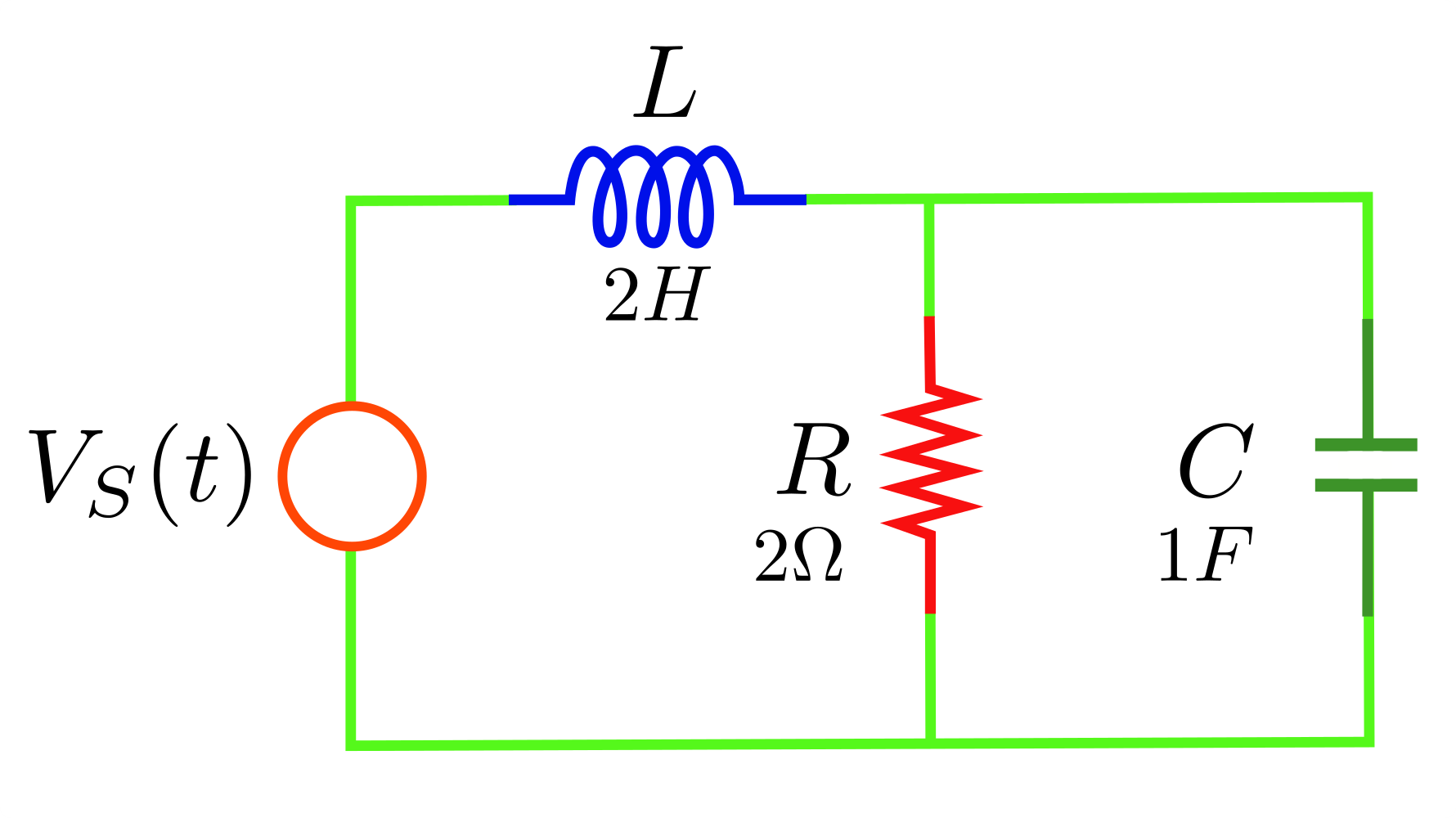
El sistema eléctrico para modelar en espacio de estados de la figura 10, Sistema eléctrico, tiene los mismos elementos que los del Ejemplo 3 de esta unidad de aprendizaje: una inductancia L, una resistencia R y un capacitor C, alimentados por una fuente de voltaje V_s (t) pero conectados de forma distinta. Siguiendo la teoría planteada en esta UAPA, vamos a mencionar la serie de pasos del modelado en espacio de estados de este sistema.

Paso 1

Con base en lo aprendido hasta este momento, el primer paso es determinar las variables de estado. El sistema eléctrico tiene dos elementos acumuladores de energía, por lo que la elección de las variables de estado son: el voltaje del capacitor V_c ( t ) y la corriente del inductor i_L ( t ), así, podemos escribir las variables de estado de la siguiente manera

Paso 2

En este paso se elige la variable de salida, ésta será el voltaje en el capacitor V_c ( t ), que como se puede ver es el mismo voltaje que se tendrá en la resistencia R y, así ya tenemos dos de los pasos de nuestra metodología.

Paso 3

En este paso vamos a obtener las ecuaciones dinámicas del sistema. Es necesario recurrir a la Ley de voltaje de Kircchoff a lo largo de la malla y a la Ley de corrientes de Kircchoff en el nodo A (estas dos leyes pueden ser consultadas en: https://dctrl.fi-b.unam.mx/academias/aca_ace/txt/P_00.pdf, como se muestra en las figuras 11a) y 11b), respectivamente.

Figura 11. *a) Análisis de la malla, b) análisis del nodo A*

Del análisis de la malla mostrada en la figura 11a) Análisis de la malla, sabemos que la suma de todas las diferencias de potencial eléctrico alrededor de la malla es cero, por lo tanto, podemos escribir que

Entonces, la ecuación dinámica del sistema resultante del análisis de la malla 1 es

Aquí, la ecuación (15) utiliza el voltaje del capacitor ya que, como se había mencionado, el voltaje en la resistencia es igual al voltaje del capacitor, esto es,

Este cambio se hace por conveniencia, ya que el voltaje en el capacitor será determinado por el mismo modelado, y así se evita agregar una variable al sistema. El término

determina el voltaje en la inductancia y V_S ( t ) es el voltaje de la fuente. En el análisis del nodo A, las Leyes de corriente de Kircchoff establecen que la suma de las corrientes que entran en el nodo es igual a la suma de las corrientes que salen, por lo tanto, podemos escribir que

Siendo así, la ecuación dinámica del sistema resultante del análisis del nodo A resulta en

Aquí la ecuación (16) tiene a i_L (t) que describe la corriente en la inductancia,

es la corriente en la resistencia y

es la corriente en el capacitor.

Paso 4

Trabajando con las ecuaciones dinámicas (15) y (16) se procede a escribirlas en términos del modelado en espacio de estados. Estas ecuaciones describen un sistema lineal, por lo que se pueden expresar en la forma matricial de las ecuaciones (3) y (4). Despejando los términos diferenciales de las dos ecuaciones, estas pueden ser escritas de la forma

Sustituyendo los valores de los elementos mostrados en la figura 10, Sistema eléctrico, podemos escribir la ecuación de estado x ̇(t) de la forma

En su forma expandida, al utilizar las igualdades de

en términos de las variables de estado, se obtiene la siguiente ecuación

La ecuación de salida y (t ) en forma matricial es

Así, la ecuación de estado (17) y la ecuación de salida (18) describen de forma matricial el modelado de espacio de estados del sistema eléctrico de este ejemplo.

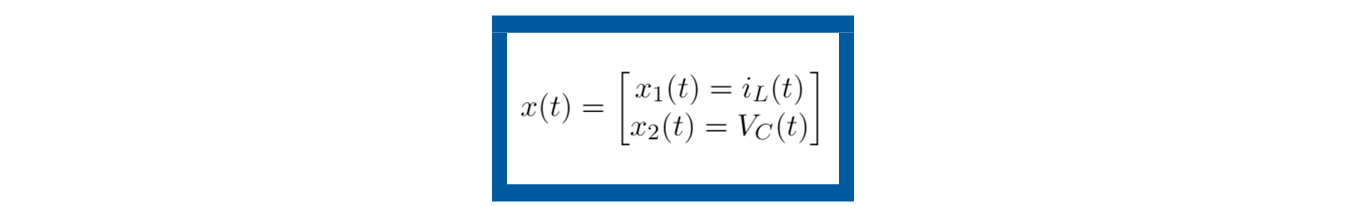
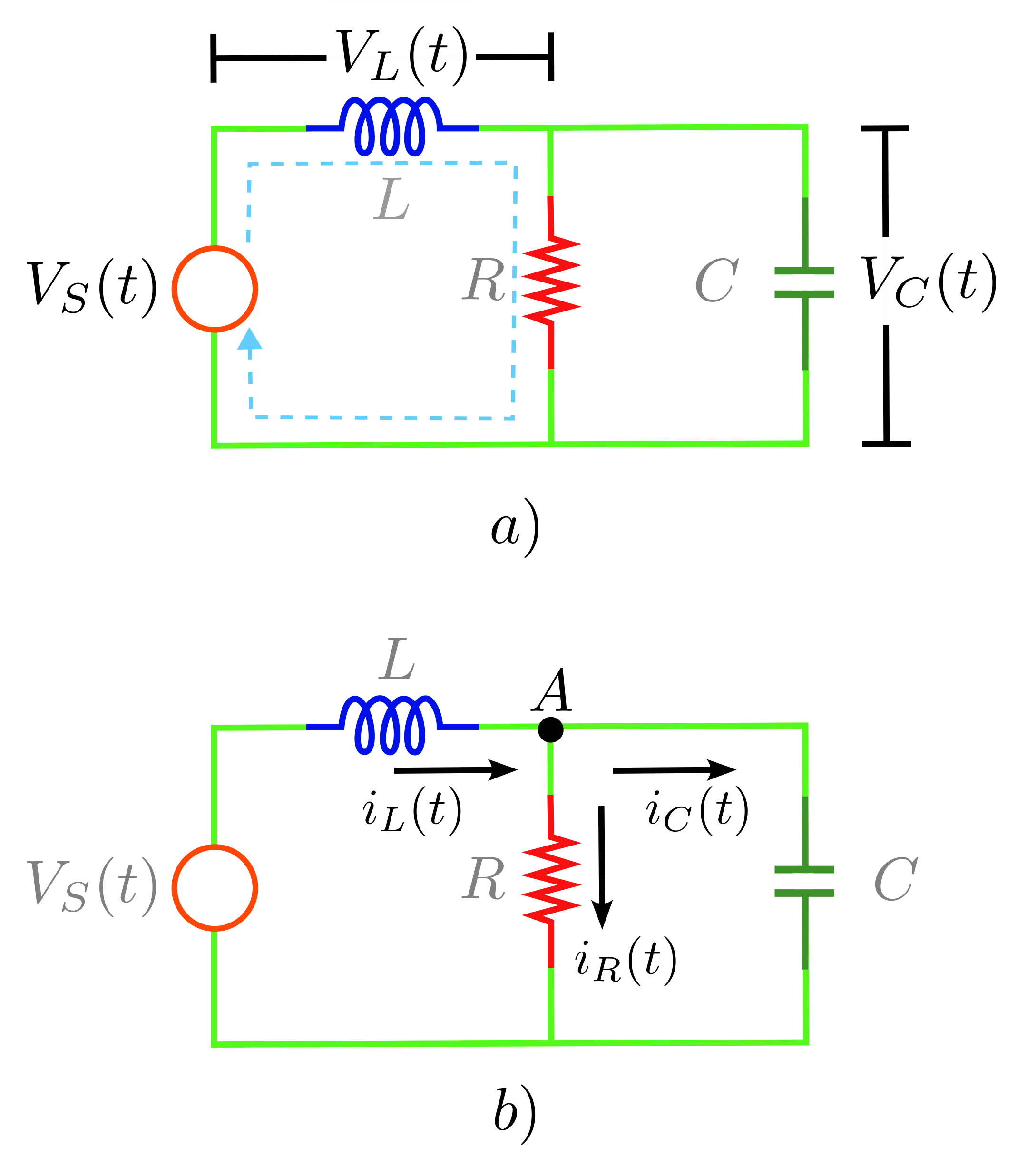
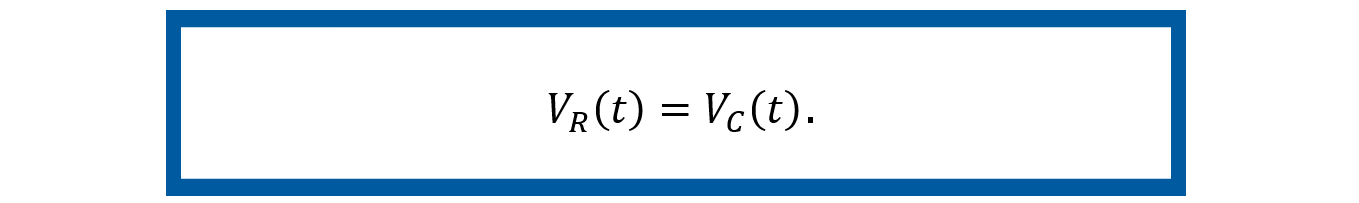
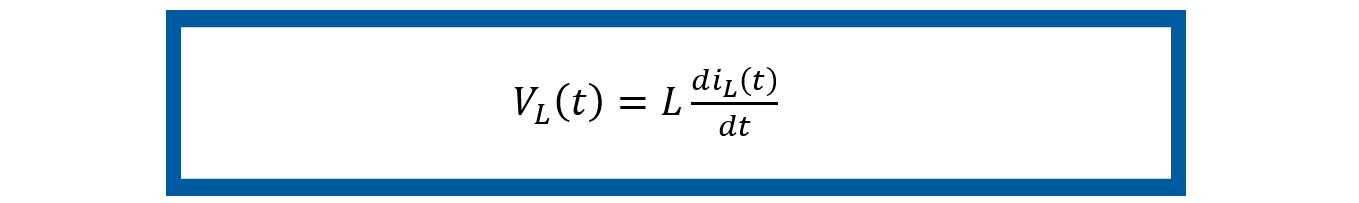
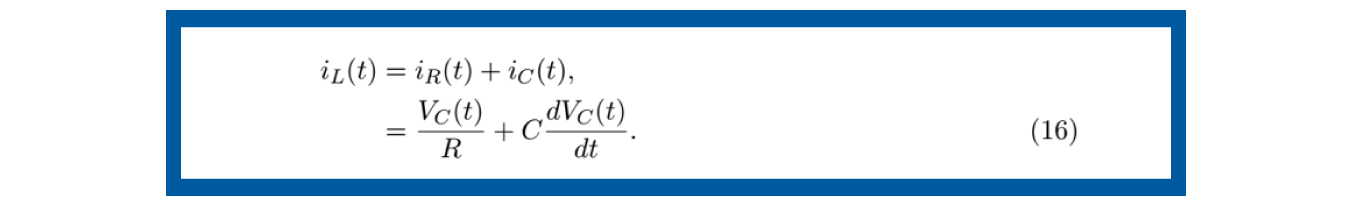
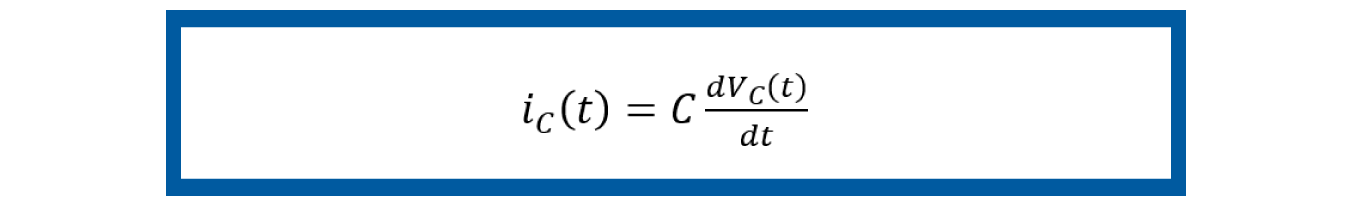
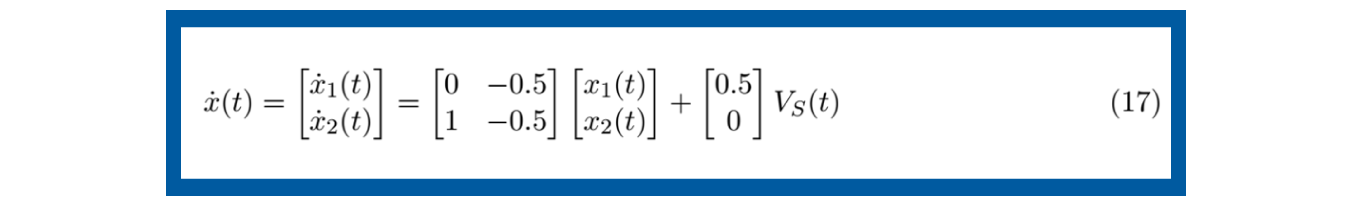
Hasta este punto, hemos explorado varios ejemplos que ilustran los conceptos clave que acabamos de aprehender. Ahora, es el momento de llevar ese conocimiento a la práctica mediante el planteamiento de un ejercicio.

Toma en cuenta que el aprendizaje activo no tiene lugar solamente entendiendo los principios o los pasos de forma estructurada, sino hasta que logres aplicarlos de manera activa.

El ejercicio que seguirá está diseñado para desafiarte y fortalecer tu comprensión de los conceptos recién adquiridos. No te preocupes si encuentras alguna dificultad al principio; la práctica constante es fundamental para el desarrollo de cualquier habilidad.

Recuerda, el objetivo de realizar este ejercicio no implica solamente encontrar la respuesta correcta, sino desarrollar tu capacidad para abordar problemas de manera independiente e ingeniosa. ¡Buena suerte y disfruta del proceso de aprendizaje activo!

Actividad de aprendizaje 1. Modelado en espacio de estados de un sistema eléctrico.

Como recordarás, el modelado en espacio de estados de un sistema eléctrico se basa en el uso de las leyes de Kircchoff de nodos y de mallas (que puedes consultar en el siguiente enlace: https://dctrl.fi-b.unam.mx/academias/aca_ace/txt/P_00.pdf), de tal manera que se obtenga una representación matemática que haga uso solamente de las variables de estado, sus derivadas y la señal de entrada.

A continuación, se presenta una actividad de aprendizaje con la cual vas a poner a prueba lo aprendido en este recurso sobre el modelado en espacio de estados. Para realizar con éxito el ejercicio tendrás que reflexionar sobre los conceptos básicos y metodología para la resolución del modelo.

Autoevaluación. La importancia de la teoría del modelado de sistemas de ingeniería en espacio de estados.

Un saludo de nuevo, estamos por concluir el estudio del tema, pero antes de hacerlo ocupémonos de la siguiente autoevaluación. Como sabes, la ingeniería de sistemas es una disciplina fundamental en el diseño y análisis de sistemas complejos, ya sea en Ingeniería Eléctrica, Mecánica, de Control o cualquier otro campo. Dentro de las temáticas fundamentales en esta disciplina se encuentra el modelado de sistemas en espacio de estados, la cual es una técnica poderosa que permite representar sistemas dinámicos en forma matricial, lo que facilita su análisis y control.

La siguiente actividad de autoevaluación consiste en una sopa de letras donde deberás buscar palabras clave relacionadas con el modelado de sistemas en espacio de estados. Estas palabras pueden incluir conceptos teóricos, ecuaciones fundamentales, métodos de análisis y otros términos relevantes vistos y analizados en este tema. Al completar la sopa de letras podrás autoevaluar tu comprensión de los conceptos básicos y tu capacidad para identificar y recordar los términos clave asociados con este tema.

Te sugiero leer cuidadosamente cada uno de los reactivos presentados para encontrar la respuesta correcta.

Para visualizar y realizar este ejercicio es necesario que lo abras desde una PC o Lap top.

Fuentes de información

Básicas

Domínguez, S., Campoy, P., Sebastián, J. M., Jiménez, A. (2006). Control en el espacio de estado. Pearson Prentice Hall.
Kuo, B. C. (1996). Sistemas de control automático. Prentice Hall.
Chen, C. T. (1995). Analog and digital. Control system design: transfer-function, state-space, and algebraic methods. Oxford University Press, Inc.
Serway, R. A. y Jewett, J. W. (2008). Física para ciencias e ingeniería. Cengage Learning.